Kirottu joukko-oppi, siunattu joukko-oppi
 Joukko-oppi, englanniksi ’set theory’, on matematiikan haara, joka tutkii joukkoja. Sen perustaja Georg Cantor määritteli joukon siten, että se on toisistaan erotettavien objektien [olioiden] yhdistelmä. Tämä määritelmä toimii näkemyksellisesti useimmiten edelleen, vaikka joukon muodollinen määritteleminen osoittautuikin myöhemmin monimutkaisemmaksi. Joukko-oppi, englanniksi ’set theory’, on matematiikan haara, joka tutkii joukkoja. Sen perustaja Georg Cantor määritteli joukon siten, että se on toisistaan erotettavien objektien [olioiden] yhdistelmä. Tämä määritelmä toimii näkemyksellisesti useimmiten edelleen, vaikka joukon muodollinen määritteleminen osoittautuikin myöhemmin monimutkaisemmaksi.
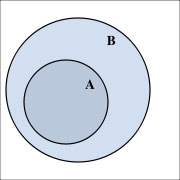
Objekteja, tai olioita kutsutaan joukon alkioiksi, ja ne voivat perustua ihmisen havaintoon tai ajatukseen. Oleellista on tietää mistä tahansa objektista, kuuluuko se tiettyyn joukkoon vai ei. Joukkoja voidaan havainnollistaa niin sanotuilla Venn-diagrammeilla, joista on esimerkki oikealla.
Joukko-oppia on pidetty eräänlaisena matematiikan esperantona eli yleismaailmallisena modernin tieteellisen matematiikan esittämismuotona. Suomen yleiskielessä joukko-opilla viitataan usein 1970-luvun huonomaineiseen koulutuskokeiluun, jossa joukko-oppi tuotiin uutena metodina matematiikan perusteiden opetukseen.
Tyhmentyneet vanhemmat
Kun Suomessa vielä vallitsi rinnakkaiskoulujärjestelmä, kansakoulu ja oppikoulu, kansakoulussa opetettiin laskentoa ja mittausoppia. Oppikoulussa opetettiin taas matematiikkaa, johon kuului muun muassa algebra ja geometria.
Niin sanottua uutta matematiikkaa ja sen perustana olevaa joukko-oppia alettiin opettaa Suomen kouluissa 1970-luvun alussa jo muutamaa vuotta ennen kuin siirryttiin peruskouluun. Uuden matematiikan liike oli lähtöisin Ranskasta, mistä se levisi nopeasti muualle Eurooppaan ja Yhdysvaltoihin. Uudistusliikkeen tavoitteena oli saada koulumatematiikka mahdollisimman lähelle korkeampaa, tieteellistä matematiikkaa.
Sekä peruskoulu että joukko-oppi rantautuivat Suomeen Ruotsista. Uuden opin kannattajat olivat niin sanottuja edistyksellisiä ihmisiä, kun taas vastustajia pidettiin taantumuksellisina. Taistelu muutoksen ympärillä oli kiivasta osittain senkin takia, että suomalainen yhteiskunta oli tuolloin kaikkein politisoituneimmillaan ja polarisoituneimmillaan sitten vuoden 1918.
Uudistuksen täytäntöönpano oli ripeä. Opettajat koulutettiin joukko-oppiin vain lyhyillä pikakursseilla. Lasten vanhemmista ei taas ollut mitään apua muutoksen omaksumisessa, sillä heille ei joukko-oppia ollut koskaan opetettu.
Oppirakennelma
Joukon käsite on kuitenkin nykyisin tärkeä kaikilla matematiikan alueilla. Matemaattisesti tärkeimpiä ovat niin sanotut lukujoukot, joiden alkiot ovat lukuja.
Joukot voidaan esittää luettelomuodossa tai tietyn säännön avulla. Joukko voi lisäksi olla päättyvä tai päättymätön eli äärellinen tai ääretön. Alkioiden järjestyksellä ei joukoissa ole merkitystä. Toisin on esimerkiksi järjestettyjen parien ja lukujonojen tapauksessa.
Joukko-oppi jaetaan yleisesti naiiviin joukko-oppiin ja aksiomaattiseen joukko-oppiin. Aksiomaattisen joukko-opin kehittämiseen vaikutti Russelin paradoksi. Se osoitti, ettei joukkoa voi määritellä yksinkertaisesti alkioiden kokoelmaksi, mikä täten kaatoi naiivin joukko-opin.
Joukkoa, jonka alkiot ovat joukkoja, kutsutaan perheeksi tai joukkoperheeksi. Esimerkiksi sigma-algebra on joukkoperhe.
Esimerkkejä:
1. Lukujen 1 ja 10 välillä olevien alkulukujen joukko on {2, 3, 5, 7}
2. Luonnollisten lukujen joukko, {0, 1, 2, 3, …} tai {1, 2, 3, …} on määritelmästä riippuen ääretön lukujoukko.
3. Parillisten luonnollisten lukujen joukko on {0, 2, 4, 6, 8, ...} tai {2, 4, 6, 8, …}
4. Päävärien muodostama joukko on {punainen, keltainen, sininen}.
Lisämääritelmiä:
-
Pääjoukko
-
Osajoukko
-
Samuus
-
Mahtavuus
-
Tyhjä joukko
Operaatioita:
-
Unioni eli yhdiste
-
Leikkaus
-
Joukkoerotus
-
Karteesinen joukko
-
DeMorganin lait
-
Potenssijoukko
Uho ja unho
Matematiikan opiskelu joukko-opin menetelmällä tarkoitti sitä, että numerot korvattiin opetuksen alkuvaiheessa alkioilla ja joukoilla sekä yhteenlasku unioneilla. Luvut ja niillä suoritettavat laskutoimitukset opetettiin myöhemmässä vaiheessa joukko-osan käsitteiden avulla. Muutos näkyi selkeimmin matematiikan kirjojen sisällöissä. Kirjoista tuli kuvapainotteisia.
Joukko-opin kouluopetusta kohtaan esitettiin runsaasti kritiikkiä. Eräässä vaiheessa jopa katsottiin, että tätä menetelmää opetettiin matematiikan avulla eikä toisin päin. Uusi matematiikka miellettiin kokonaisuudessaan liian teoreettiseksi, joka ylikorosti symboleja sekä nimityksiä ja oli käytännön elämälle vieras.
Oppisisällöt olivat sitä paitsi tuntikehykseen verrattuna liian laajat, eikä uusi jaottelu johtanut odotettuihin oppituloksiin. Uuden matematiikan kukoistusvaihe kesti vain vuoteen 1976, jolloin Kouluhallitus esitteli uusvanhan matematiikan perusoppiaineen. Joukko-opin käytöstä matematiikan alkeiden opetuksessa luovuttiin virallisesti vuonna 1983.
Joukkoihin liittyviä symboleita

(Wikipedia 2008b)
Että se siitäkin koulu-uudistuksesta sitten. Onneksi.

N.V.: Ei matemaattinen lahjakkuus ole suinkaan sitä, että tietää, että yksi ynnä yksi on yk… hm kaksi. (Veikko N:o 3 1970, 35)

Säde: Tämä kompassi näyttää, että pohjoinen on tuolla. Hm! Tämä toinen taas, että pohjoinen olisi tuolla. Hmmm! Minun mielestäni pohjoinen on kylläkin noiden välissä.
(Veikko N:o 4 1970, 35)
|
